Analytical Model of Radar Scattering from Ocean Surface
Calculation of the radar echo from a rough sea is not a simple task due to the very complex nature of both sea-surface roughness and its interaction with the radar pulses. The short, centimeter-scale waves that are responsible for radar backscattering at moderate incidence angles are superimposed on a continuum of longer waves, ranging in scale from tens of centimeters to hundreds of meters, which travel in various directions. Even numerical solutions of this statistical problem in three dimensions are beyond the abilities of today's computers.
To simplify the problem, "two-scale" or composite-surface models have been tried. This approach combines two "classical" methods of wave-propagation theory: the small-perturbation method and the tangent-plane method. However, due to insufficient accuracy, the two-scale method makes it difficult to retrieve winds accurately enough. We developed an analytical model called the small-slope approximation (SSA) [1, 2] that does not have any fitting parameters and uses surface slope as a small parameter. The SSA gives an explicit expression for a scattering cross section in terms of the spectrum of surface roughness (in the case of Gaussian statistics). Originally, the empirical sea roughness spectrum proposed in [3] was employed in the SSA numerical codes for calculations of scattering cross sections of the ocean surface. The spectrum was developed based on available field and wave-tank measurements along with physical arguments. The SSA numerical codes can be easily updated as new spectral models become available.
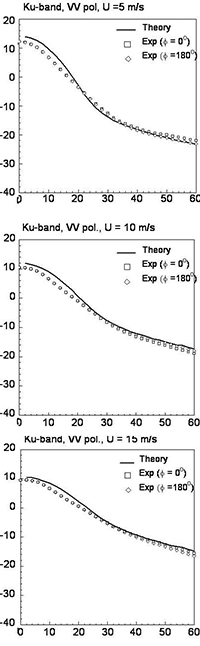
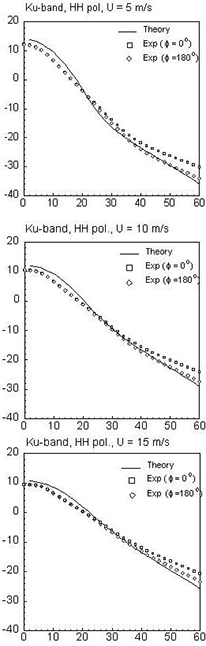
The results of numerical calculations for Ku- and X- band were compared with existing experimental data. Evaluation of the backscattering cross section with the help of the SSA using an average sea-roughness spectrum coincides with average experimental data to 1-2 dB accuracy (see Fig. 1A) with the exception of HH polarization at large incidence angles (Fig.1B).
| A | B | C |
 |
 |
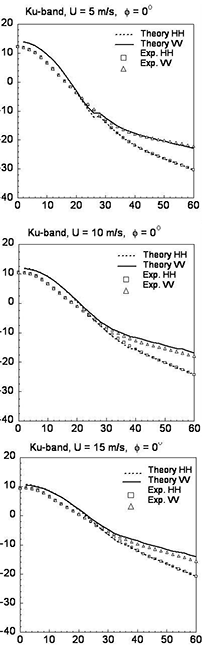 |
| Figure 1. (A) Comparison between theoretical (without the effect of breaking waves) and average experimental results for the Ku-band and VV-polarization; (B) Comparison between theoretical (without the effect of breaking waves) and average experimental results for the Ku-band and HH-polarization; (C) Comparison between theoretical (including the effect of breaking waves) and average experimental results for the Ku-band and both HH- and VV-polarization. | ||
The HH polarization discrepancy led us to hypothesize that scattering from Bragg resonant waves is not the only mechanism involved, and reflections from steep slopes of breaking waves in the along-wind direction should be taken into account. Unfortunately, the probability distribution function P of slopes is known only over relatively small values of the slope. The best guess for P of large slopes for the case of the upwind direction based on fitting calculated cross sections to empirical ones within 1–2 dB accuracy for all winds, incidence, and azimuthal angles and polarizations (see Fig. 1C) appeared to be reasonable (Fig. 2, see [2] for details). For calculation of backscattering from steep breaking waves, it was assumed that the geometric optics approximation is valid.
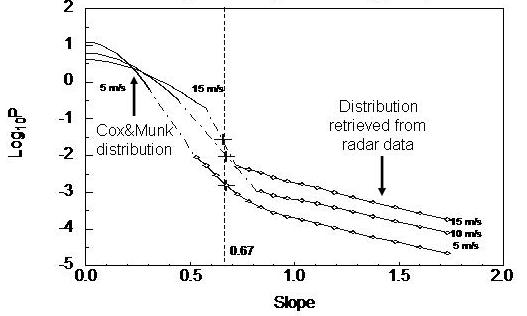
A practical implication of this model is its potential as a method to increase the accuracy of wind-speed retrieval from scatterometric measurements similar to the two-scale-model algorithm proposed in [7], but instead based on the analytical approach discussed above.
Another outcome of this part of the work is finding that scattering from breaking waves alone can be used for the measurement of the near-surface wind vector especially beyond the wind-speed range of currently used scatterometric techniques. In particular, this type of scattering is characterized by “spikes,” in which the signal at horizontal polarization exceeds the signal at vertical polarization for short periods of time, and the Doppler spectrum appears to be wider as compared to simulations, especially at horizontal polarization. Analytical approaches to the problem fail in this case because the breaking wave is a strongly non-linear object currently lacking reliable analytical description. Instead, the problem of scattering of radar waves from breaking surface waves can be successfully addressed by means of direct numerical simulations.
References
- Voronovich, A.G., 1994, Wave Scattering from Rough Surfaces, Berlin, Springer, pp. 147-208.
- Voronovich, A.G. and V. U. Zavorotny, 2001, Theoretical model for scattering of radar signals in Ku- and C-bands from a rough sea surface with breaking waves, Waves Random Media, 11, 247-269.
- Elfouhaily, T., B. Chapron, K. Katsaros, and D. Vandemark, 1997, Unified directional spectrum for long and short wind-driven waves, J. Geophys. Res., 102, 15,781-15,796.
- Cox, C. and W. Munk, 1954, Measurement of the roughness of the sea surface from photographs of the sun’s glitter, J. Opt. Soc. Am., 44, 835-850.
- Cox, C. and W. Munk, 1954, Statistics of the sea surface derived from sun glitter, J. Mar. Res., 13, 198-227.
- Omuircheartaigh, I. G. and E. C. Monahan, 1986, Statistical aspects of the relationship between oceanic whitecap coverage: wind speed and other environmental factors, In Oceanic Whitecaps and Their Role in Air–Sea Exchange Process, Ed. E. C. Monahan and G. MacNiocaill, Dordrecht, Reidel, 125-128.
- Janssen, P.A.E.M., H. Wallbrink, C. J. Calkoen, D. van Halsema, W. Oost, and P. Snoeij, 1998, VIERS-1 scatterometer model, J. Geophys. Res., 103, 7,807–7,831.