The Technical Details: Determining Delta Values
Stable Isotopes
When we talk about the isotopic ratio in a sample, we talk about the delta value. Let's look at how a delta value is actually calculated:
- The first step in figuring out the δ13C for a sample is to find the ratio of 13C to 12C within the sample.
-
Next compare (by dividing) this ratio to the ratio of 13C to 12C in a standard.
- There is a specific standard, with a known, unchanging ratio of 13C to 12C that all laboratories use in their comparison. For the stable carbon isotopes, this standard is a limestone (called Pee Dee Belemnite—or PDB) from South Carolina. Although PDB is no longer run as the standard, other carbonates (with a known, unchanging 13C to 12C ratio) are used and compared on the PDB scale. The carbonate standard is reacted with an acid to create gaseous CO2, so that the sample and standard are both in the same phase.
- Often the sample and standard may have very similar ratios of the two stable isotopes, which will give you a value very close to (but not exactly) 1.
 Two sample bellows are used so that the sample is compared to a standard
Two sample bellows are used so that the sample is compared to a standard -
Many samples that actually have different ratios of 13C to 12C will give what seems like similar values (say, for example, 0.99 and 0.98). These samples do have different isotopic ratios, but this is hard to see when they only differ after the decimal point. To make this difference easier to see, 1 is subtracted from this value, and then this new calculation is multiplied by 1,000 to give the actual δ13C of the sample.
- This makes it much easier to see the difference between two samples. For the ratios of 0.99 and 0.98, the delta values are -10‰ and -20‰ respectively.
The equation for this is:
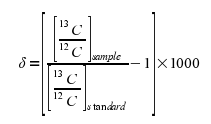
Making the Values More “Friendly”
Even when comparing samples with ratios of 13C to 12C of 0.99 and 0.98, the delta notation is much easier. Well, when we look at ratios that atmospheric scientists actually study, it becomes infinitely easier to compare using delta notation–in fact it would be too difficult without!
| Carbon Pool | 13C | Actual ratio of 13C to 12C |
|---|---|---|
| Ocean & Atmosphere | -8‰ | 0.011142 |
| Terrestrial Biosphere | -26‰ | 0.010945 |
| PDB Standard | 0‰ | 0.011237 |
Why Go Through This Much Work?
This seems like an awful lot of calculations when you can just look at differences among samples in their 13C to 12C ratios and ignore all of the calculation steps. The reason that it is conventional to compare to a standard (and then continue on to the next steps in order to get a more ‘friendly’ value) is so that it is easier to compare results both among isotope laboratories and within a single laboratory over a long time period. It is impossible to have an isotope ratio mass spectrometer that perfectly finds the ratio of 13C to 12C in a sample.
Isotope ratio mass spectrometers measure relative isotopic ratios much better than actual ratios. By comparing to a standard, the precision of the data values are much, much better since all values are relative to a given standard. For example, if the ratio for both the sample and standard are overestimated (or underestimated) by the same relative amount, then dividing the two values will account for this, making it possible to compare δ13C among laboratories all across the world.
Radiocarbon Δ14C
The formula for determining the Δ14C of a sample is similar to δ13C:
The difference is in the term FN[x], which is still a comparison of the sample to a standard. However, after this comparison, several other calculations occur to find FN[x].
- The ratio is corrected for “background” 14C counts, where atoms or molecules that were accidentally and incorrectly identified as 14C are no longer included.
- The ratio is additionally corrected for the small amount of radioactive decay between the time the sample was collected and the time it was measured, so that the Δ14C at the time of collection rather than the time of analysis is reported.
- The final difference is that Δ14C is normalized, where the effect of fractionation is removed. That is, we know from the 13C measurements that, for example, when carbon dioxide is photosynthesized by plants, it fractionates, resulting in proportionately less 13C in the plant. The same thing happens to 14C, so plants have proportionately less 14C than the atmosphere does. If we know how much 13C fractionation occurs, we can calculate precisely how much 14C fractionation there is. We then calculate how much 14C would have been in the sample if it had not fractionated. This is the Δ14C. Why go to all this trouble? The main reason is that for radiocarbon dating, scientists want to study how much 14C has decayed, not how much has fractionated, and this normalization allows them to do just that. The second reason is that it makes it easier to understand the 14C in the atmosphere – now when plants photosynthesize CO2, the Δ14C value in the atmosphere does not change. Of course, we can always reverse the calculations to discover the amount of 14C without applying this normalization, and this is written as δ14C.
