APPENDIX F
COMPUTATION OF COS Z AND mu FOR SUN AND MOON
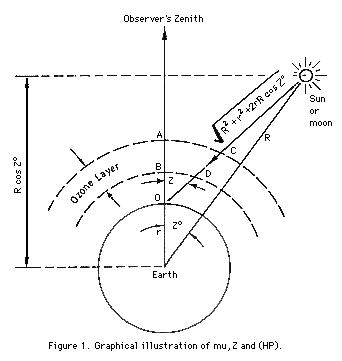
The dimensionless quantity, mu, is the ratio of the ozone layer path length traversed by a ray of light emanating from the sun or moon at the time of observation to the vertical path length. As illustrated in Figure 1, mu is equal to CD/AB. In practice, mu values are obtained from a table which relates cos Z and mu. The angle, Z, shown in the figure is referred to as the celestial body's zenith angle (or distance). At certain times during the day, Z may change rather quickly; hence, it is necessary to time observations to within ±10 seconds to preserve sufficient accuracy in the computed mu values.
Cos Z values are obtained by solving the astronomical triangle equation
Notice in Figure 1 that because of the great distance separating the sun and earth the zenith angle Z is very nearly equivalent to the angle Z* (the difference in angles is greatly exaggerated in the diagram). Hence, a solution of equation (1) yields cos Z at once. The moon, on the other hand, is relatively near the earth. As a result, Z is appreciably greater than Z*. The procedure here is to compute cos Z* from equation (1), then apply it to a parallax correction, Deltacos Z*, to obtain cos Z.cos Z* = cos(theta)cos(delta)cos(phi) + sin(delta)sin(phi) . (1)
The parallax correction is obtained from a table (given in Appendix G) which relates Deltacos Z* to (HP), where the latter symbol denotes the moon's horizontal parallax obtained, e.g., from the Nautical Almanac, United States Naval Observatory, for the time of observation. The table has been computed from equation (4) given below, which is derived as follows. With reference to Figure 1,
R cos Z* - r cos Z = ---------------------------- (2) sqrt(R2 + r2 - 2rR cos Z*)
where R is the separation of the earth and moon centres and r is the radius of the earth. By definition
(HP) = r/R [radians]. (3)
Dividing the numerator and denominator of the right hand side of equation (2) by R gives
cos Z* - (HP) cos Z ~ ------------------------ R >> r sqrt(1 - 2(HP) cos Z*) ~ cos Z* - (HP) sin' Z*.
[Note: Computational examples presented in this Appendix utilize astronomical data from the Nautical Almanac for 1961, United States Naval Observatory.]
Finally,
Deltacos Z* ~ Cos Z - Cos Z* ~ -(HP) sin2 Z* . (4)
The quantities theta, delta and phi in equation (1) are, respectively, the hour angle and declination of the luminescent celestial body, and the latitude of the observer's station. So that the observer comprehend fully the significance of equation (1), a brief introduction to astronomical concepts is presented in Appendix H and Appendix I with which the reader is encouraged to become familiar before proceeding to the next section which deals with the method of computing cos Z and mu.
Examples of Computing mu
On the following two pages are shown mu computations for hypothetical observations made on the sun and moon at Sterling, Virginia, U.S.A., and Hallett Station, Antarctica.


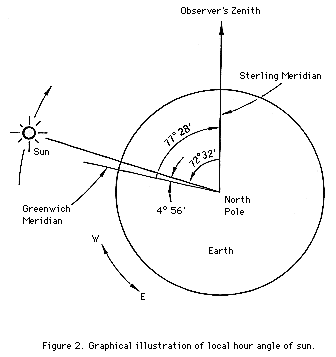
Consider first the computation of mu for the DS observation made at Sterling on July 9, 1961. Since the observation was made at 12h 24m 47s GMT, we turn to page 137 of the Nautical Almanac for the Year 1961 where the sun's declination is listed for every hour GMT. At 12h the declination is +22° 21.5' whereas at 13h it is 22° 21.2'. By interpolation, the declination at the time of observation was +22° 21' to the nearest minute. (Note that care must be taken in interpolating since the declination may be increasing or decreasing with time depending on the time of year.) At 12h GMT the Greenwich hour angle (GHA) of the sun is given as 358° 43.8'. Turning to page xiv of the Nautical Almanac we find that in 24m 47s the change in the sun's GHA is 6° 11.8'. Therefore, at the time of observation the sun's GHA was 358° 43.8' + 6° 11.8' = 364° 56', or, subtracting 360°, it was 4° 56'. Notice that the sign of the GHA is (implied) positive. This means that the sun is 4° 56' west of the Greenwich meridian. But Sterling is also located west of the Greenwich meridian at a longitude of 77° 28'. Hence, the local hour angle theta of the sun at Sterling at the time of observation was 4° 56' - 77° 28' = -72° 32'. The situation is pictured in Figure 2. Since the cosine function is an even function (that is, cos(theta) = cos(-theta)), we find from the cos theta (hour angle) table given in Appendix G that cos theta = cos (-72° 32') = 0.3001. Cos(delta)cos(theta) is obtained from a table of cos(delta)cos(theta) vs. delta provided for each station, as is sin(delta)sin(phi). Finally, using equation (1) cos Z is obtained and hence mu from a table relating cos Z and mu, also given in Appendix G.
In computing mu, it is best to tabulate the values of declination, GHA and theta as follows:
Declination GHA theta = GHA - Long 22° 21' 358° 43.8' 4° 56' 6° 11.8' -(+77° 28') ---------- ------------ 364° 56' -72° 32' -360° 00' ---------- 4° 56'
For the hypothetical direct sun observation made at Hallett Station on December 25, 1961, we have the following values of declination, GHA and theta:
Declination GHA theta = GHA - Long -23° 23' 164° 55.4' 168° 45' 3° 49.3' -(-170° 19') ----------- ------------ 168° 45' 339° 04'
Consider now the computation of mu for the hypothetical RMFI observation made at Sterling on December 23, 1961, at 6h 03m 37s GMT. From page 247 of the Nautical Almanac we find that at 6h, the declination of the moon is +19° 44.1', whereas at 7h it is 19° 42.9'. Again direct interpolation may be made to obtain the required value of the declination. Notice, however, that given next to the value +19° 44.1' is a "d" code number, d = 1.2. Turning to increments and corrections, page iii, we find that for 03m 37s the correction for d = 1.2 is 0.1. Since the moon's declination is decreasing, we find that the declination at the time of observation is 19° 44.1' - 0° 0.1' = 19° 44' to the nearest minute. The moon's GHA is obtained in a similar manner. Again from page 247 we find that at 6h GMT the GHA = 75° 12.1', and the "v" code number is 10.3. Again, for, 03m 37s the change in the GHA for the moon, as shown on page iii, is 0° 51.8' + 0.6'. (The 0.6' is read off the page corresponding to the v = 10.3 code number). Thus, the GHA for the moon is 75° 12.1' + 0° 51.8' + 0.6' = 76° 05'. Tabulating the data as in the previous examples, we have:
Declination GHA R = GHA-Long HP 19° 44.1' (d=1.2) 75° 12.1' (v=10.3) 76° 05' 55.5 -0° 0.1' 51.8' -(+77° 28') ---------- 0.6' ----------- 19° 44' ---------- -1° 23' 76° 05'
Solving equation (1) now leads to the value of cos Z* = 0.9439. To obtain cos Z, note that at the time of observation the moon's horizontal parallax (H.P.) was 55.5, as given in the Nautical Almanac. From the Table of Parallax Corrections for the Moon (Appendix G) we find that the parallax correction, Deltacos Z*, is 0.0017. Hence, cos Z = cos Z* - Deltacos Z* = 0.9439 - 0.0017 = 0.9422, and mu = 1.061.
Finally, for the hypothetical moon observation made at Hallett we have
Declination GHA theta = GHA-Long. H.P. -18° 46.2' (d=3.0) 150° 38.9' (v=4.1) 159° 16' 60.8 +0° 1.8' 8° 34.7' -(-170° 19') --------- 2.4' ------------ -18° 44' ----------- 329° 35' 159° 16'
The observer is reminded that both delta and theta can be positive or negative, depending on the time of year and location of the observer's station. Sin(delta)sin(theta) may, therefore, assume positive or negative values. Cos(delta)cos(theta) is always positive. The GHA for the sun or moon given in the Nautical Almanac is always positive.
3. Calculation of mu at Amundsen-Scott Station
Amundsen-Scott station is located in Antarctica at a latitude of nearly -90 degrees. Letting theta = -90° in equation (1) we obtain
cos Z* - sin delta. (5)
Since cos Z* ~ cos Z for observations made on the sun, it is evident that Z can be determined at once from a knowledge of the sun's declination at any time:
Z* ~ Z 90° + delta. (6)
Mu is then simply obtained from a table relating cos Z and mu (see Appendix G).
For moon observations, the horizontal parallax has to be taken into account. Cos Z* is computed first: then the appropriate value of Deltacos Z* is subtracted from cos Z* to give cos Z.
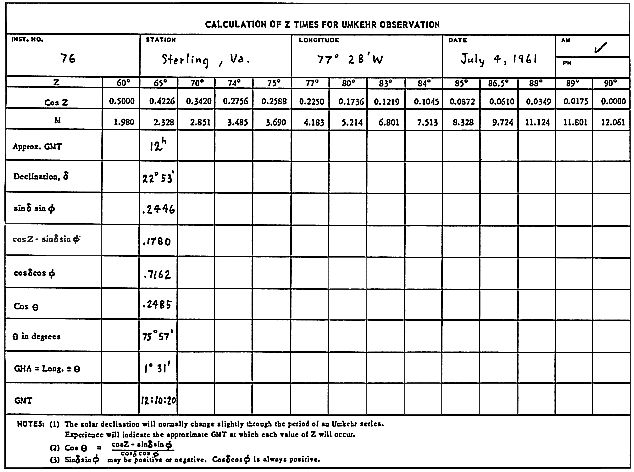
4. Calculation of Z Times for Umkehr Observations
In Section 6.3.1 it was pointed out that in processing Umkehr data, the N values of interest are those corresponding to discrete zenith angles of the sun. The zenith angles of interest are shown on a form on the following page. To compute the precise times at which these angles occur during any one-half day, the usual mu computations are performed on this form in reverse, as illustrated. Note that it is necessary for the observer to "guess" the approximate time at which a particular zenith angle occurs in order to be able to estimate the sun's declination.
5. Cos Z Determinations by Computer
(a) To facilitate the application of digital computers and small calculators to problems of astronomy, the Almanac for Computers (see, for example, Dogett et al., 1978) is available in which polynomial approximations replace the fixed interval tabulations of the Nautical Almanac. Using these expressions it is possible to calculate, with minimal loss of precision, basic astronomical data, including Greenwich hour angle and solar declination, for specific locations and times. A drawback to use of this Almanac is that it has been available only since 1978; also, since it is issued on a yearly basis, mu computations for several years in advance cannot be made.
(b) Yallop (1977) and Sinclair and Yallop (1977) have devised computer algorithms for computing solar hour angles and declinations corresponding to a precision in sun positions of 1' and 0.5' of arc. The algorithms given on pages 104 to 106 are based on a machine algorithm for processing calendar dates by Fliegel and Flandern (1968), and provide information of adequate precision for the processing of total ozone data for several centuries around 1980.
i Definitions
Julian day number = number of days elapsed since 12hii VariablesJulian date = Julian day number followed by the fraction of a day elapsed since the preceding noon.
D = number of days from 1900.0 (Julian date 2415020.0)
T = number of Julian centuries from 1900.0 = D/36525
L = mean longitude of sun in degrees
E = equation of time (in seconds of time)
epsilon = obliquity of the ecliptic
alpha = right ascension of sun (apparent) in degrees
delta = declination of sun (apparent) in degrees
GHA = Greenwich hour angle of sun (in degrees)
UT = Universal time which is equivalent to GMT in this context (in degrees)
iii Formulae
D = Julian date - 2415020
T = D/36525
L = 279.697 + 36000.769T
E = - (93.0 + 14.23T - 0.0144T2)sin L - (432.5 - 3.71T - 0.2063T2)cos L
+ (596.9 - 0.81T - 0.0096T2)sin2L - (1.4 + 0.28T)cos 2L
+ (3.8 + 0.60T)sin3L + (19.5 - 0.21T - 0.0103T2)cos 3L - (12.8 - 0.03T)sin 4L
tan epsilon = 0.43382 - 0.00027T
alpha = L - E/240
tan delta = tan(epsilon) sin(alpha)
GHA = UT + E/240 + 180
iv Worked Example
Find GHA and declination of the sun on 1976 August 8 at 6h UT
D = 27978.75
T = 0.7660164
L = 136.877°
E = -335.4 in seconds of time (= -1.397°)
tan epsilon = 0.433613
alpha = 138.274° = 138° 16.4'
delta = 16.098° = 16° 5.9'
GHA = 268.603° = 268° 36.2'
B D YALLOP
77-01-28
i Definitions
I = year of date
J = month (January = 1, February = 2, etc)
K = day of month
UT = Universal time in hours
D = time elapsed in days, since 1900 Jan 0d at
Greenwich noon = JD2415020.0 to date and time required
The formula given below is intended for a calculator which has a function called INT which removes the fractional part of a number. The formula has been derived from an expression written in the computer language of Fortran and was first given by H F Fliegal and T C van Flandern in the Journal of the Association for Computing Machinery, (1968), 11, 659.
ii Formulae
Compute
A = (J - 14)/12
B = INT(A)
C = 1461(I + 4800 + B)/4
U = INT(C)
E = 367(J - 2 - 12B)/12
V = INT(E)
G = (I + 4900 + B)/100
H = 3 INT(G)/4
W = -INT(H)
D = K- 2447095.5 + U + V + W + UT/24
where INT(X) means take the integer part of X
iii Worked Example
Find D on 1976 Feb 3 at 6h UT
I = 1976 J = 2 K = 3 UT = 4
A = -1 B = -1 C = 2474568.75
U = 2474568 E = 367.0 V = 367
G = 68.75 H = 51.0 W = -51
D = 27791.75
epsilon = 23.441°
e = 0.0167
D = time in days from 1900 Jan. 0.5d to instant of observation
L = 279.691° + 0.9856 4735°D remove multiples
g = 358.48° + 0.9856 003°D of 360°
lambda = L + (2e sin g + 1.25e2 sin 2g) x 57.296 conversion factor from
radians to degrees
sin(lambda) cos(epsilon) calculate alpha using x,y->r,theta conversion.
tan(alpha) = ------------------------ x = cos(lambda), y = sin(lambda) cos(epsilon).
cos(lambda) Then theta = alpha.
This gives correct quadrant and avoids
singularity at lambda = 90°.
Then :
tan Dec. = tan(epsilon) sin(alpha)
GHA = GMT (in degrees) + 180° + L - alpha.
(multiply GMT in hours by 15 to convert to degrees).
Example. To calculate GHA and Dec. of Sun at 1976 August 8, 6h GMT.
D = 27978.75
L = 136.8718°
g = 214.344°
lambda = 135.8108°
alpha = 138.2713°
Then :
Dec. = 16.0981° = 16° 5.9'
GHA = 268.600°' = 268° 36.0'
E = L - alpha where E is the equation of time in degrees.
Multiply E by 4 to convert to minutes of time.
A T Sinclair
B D Yallop
77-08-01
6. References
Doggett, E. L., G. H. Kaplan, and P. K. Seidelmann, Almanac for Computers for the year 1978,
Nautical Almanac Officer, United States Naval Observatory, Washington, D.C., 70 pp. 1978.
Fliegal, H. F., and T. C. van Flandern, A machine algorithm for processing calendar dates,
Jour. Assoc. Computing Machinery, 11, 657, 1968.
Sinclair, A. T., and B. D. Yallop, Position of the sun to accuracy of 0.5' of arc in period
1975-2000, H. M. Nautical Almanac Office, Royal Greenwich Observatory, Herstmonceux
Castle, Hailsham, Sussex BN27 1RP, 1977.
The Nautical Almanac for the year 1961, United States Naval Observatory. Available from the
Superintendent of Documents, U.S. Government Printing Office, Washington, D.C. 20402,
310 pp., 1961.
Yallop, B. D., Position of the sun to 1' of arc precision, H. M. Nautical Almanac Office,
Royal Greenwich Observatory, Herstmonceux Castle, Hailsham, Sussex BN27 1RP, 1977.
Return to Table of Contents
Forward to Appendix G. Tables Used in Computing mu