APPENDIX C

---

CALIBRATION OF THE DOBSON SPECTROPHOTOMETER OPTICAL WEDGE

          The original method devised by G. M. B. Dobson (1957b) for calibrating the spectrophotometer optical wedge involved the use of a two-lamp unit as well as a rhodiumized plate. In recent years powerful new lamps have become commercially available which permit optical wedge calibration by the two-lamp method alone.

          In Canada, the optical wedge calibration unit used consists of a water-cooled lamp holder containing two 250-watt tungsten-halogen lamps operated at 24.0 volts d.c. A prism deflects the light beams so that they appear to originate within the spectrophotometer's light acceptance cone. The light beams are made to enter the instrument individually or in combination by a shutter mechanism. In the U.S.A., an air cooled two-lamp unit is in use that contains a shutter mechanism and two 600-watt tungsten-halogen lamps operated at approximately 100 volts a.c. At the WMO International Comparison of Dobson Ozone Spectrophotometers held in NOAA, Boulder, Colorado in August 1977, it was shown that the two kinds of lamp units yield essentially identical results.

          Procedure for calibrating a spectrophotometer optical wedge by the two-lamp method and reducing the calibration data by hand is given in Sections 1 and 2 below. In Section 3, information is provided concerning reduction of the calibration data by computer.

1. Experimental Procedure - Two-Lamp Method

          The ground quartz plate is fitted above S₁ and the two-lamp unit is positioned symmetrically over the spectrophotometer inlet window. The two-lamp unit must be rigidly fixed on the instrument so that it cannot move during measurements, since a movement of 0.25 cm will change the relative illumination of the two lamps appreciably. The lamps and S₁ are covered so that no light can enter S₁ except from the two lamps.

          A small lamp with a ground glass diffuser is fitted immediately behind slit S₄. This is done by removing the optical wedge holder unit from the spectrophotometer and replacing the lens covering slit S₃ by the S₄ lamp mounting bracket from which the lamp holder has been unscrewed. After repositioning the optical wedge holder unit within the instrument, the S₄ lamp and holder are screwed into the lamp bracket.

          The initial procedure is as follows. Allow the lamps to warm up for about 10 minutes before starting the wedge calibration by burning them at their rate voltage. Set Q levers for A wavelengths. Set R-dial at about 5°. Light lamp X only (i.e., prevent Y lamp light from reaching the GQP by means of the shutter) and adjust the voltage on lamp S₄ so that the galvanometer reads zero. Now light lamp Y only, leaving the S₄ lamp untouched, and adjust the voltage on lamp Y to give zero galvanometer deflection again.

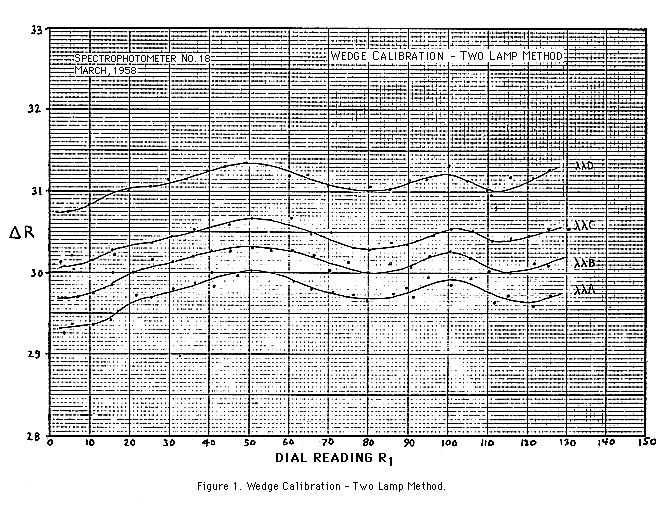
          Begin calibration of the wedges as follows. Light lamp X alone and obtain an R-dial reading, R₁, by recording a 15-second trace on the waxed chart. Light lamps X and Y together and obtain another R-dial reading, R₂. Light Y lamp alone and obtain a third R-dial reading, R'₁. (R₁ and R'₁ are later averaged and subtracted from R₂ to give DeltaR.) Now set the R-dial to about 10° and decrease the voltage on the S₄ lamp to give approximately zero galvanometer deflection. Again obtain R-dial readings using first X, then X and Y, and then Y lamp(s). Repeat the procedure at 5° intervals along the optical wedge. After measurement of the traces, plot the values of R₁ and DeltaR as shown in the sample plot. in Figure 1.

          Note that the mean difference, DeltaR, corresponds exactly to a difference in density of log₁₀ I/I' = log₁₀ 2/1 = 0.3010 at the two positions of the wedge.

2. Construction of Tables Relating Dial Readings to Log I/I'

          We proceed to construct a table which will convert values of the dial readings into values of log I/I' + K where K is an arbitrary constant.

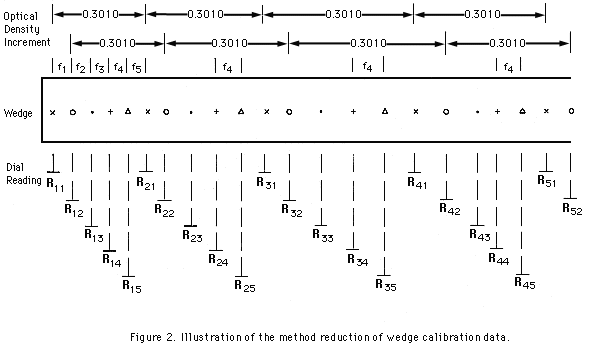
          Starting from any point on the dial close to the thin end of the wedge, let this reading be R₁₁. From the plot of DeltaR vs. R₁ (Fig. 1) we find other dial readings successively increasing in density by an amount equal to log 2 = 0.3010. Denote this series of dial points by R₁₁, R₂₁, R₃₁, R₄₁, ..... (see Fig. 2). We may next start at some other dial reading a few degrees (say 6°) away from R₁₁; let this be R₁₂ and use Fig. 1 to find another series of dial points R₁₂ R₂₂ R₃₂ ... again increasing at each step by the density of 0.3010.

          Starting at yet another dial reading (say 12° from R₁₁) we find a third series of points R₁₃, R₂₃, R₃₃ .... with the same intervals of density. In all we choose enough starting points, preferably an odd number of them, to cover the larger interval from R₁₁ to R₂₁, and find the series corresponding to each.

          The interval of density of each series is the same. It follows that the smaller density intervals between corresponding members of successive series are constant. For example, in the diagram of Fig. 2, which represents five of these series of dial readings, the increase of density from R₁₄ to R₂₄ is 0.3010, to R₃₄ is 2(0.3010), to R₄₄ is 3(0.3010) .... Similarly, from R₁₅ to R₂₅ it is 0.3010, to R₃₅ is 2(0.3010), to R₄₅ is 3(0.3010). Therefore, the small step from R₁₄ to R₁₅ represents the same increase in density (let us call it f₄) as the steps from R₂₄ to R₂₅, from R₃₄ to R₃₅, etc. In this diagram each major interval or density 0.3010 is composed of five small steps in density, f₁ to f₅, and the magnitude of each has to be determined relative to 0.3010. We know that the wedge was made to increase fairly regularly in density along its length and that any irregularities in manufacture are smoothed by the length of the slit S₃, which at each position of the dial averages a considerable portion of the wedge. We can therefore assume that the dial difference for ally major interval bears to 0.3010 approximately the same ratio as the dial difference of the central small step in that interval bears to its f. For example, (R₁₅ - R₁₄) is the central step in the major interval (R₂₂ - R₁₂), and the ratio f₄/0.3010 must be nearly equal to the ratio (R₁₅ - R₁₄) /(R₂₂ - R₁₂). Other estimates for the magnitude of f₄/0.3010 are obtained from (R₂₅ - R₂₄)/(R₃₂ - R₂₂), from (R₃₅ - R₃₄)/(R₄₂ - R₃₂) .... From these estimates along the length of the wedge a mean value of f₄/0.3010 is derived. The mean f/O.3010 ratio of each of the five small steps in density can be obtained in this way and their sum, which may differ slightly from unity because of errors in reading or irregularities in wedge gradient, should by slight adjustment be made equal to unity. All the selected dial points from R₁₁ onward can now be given a value of density in terms of 0.3010, and the values of all intermediate points can be filled in by a suitable standard method of interpolation.

          The whole method is illustrated on the Computation Form - Two-Lamp Calibration shown on the next page, which gives the data for a portion of the optical wedge in Instrument No. 18. In this instance, five (an odd number) starting points and five series were chosen. The thin end of the wedge is at a dial reading 5.0, which through successive steps of the two-lamp density interval, 0.3010, leads to 34.3, 64.1, 94.0, 123.8, and 153.3. This series appears in a row near the top of the form. The other selected starting points are 10.8, 16.6, 22.5, and 28.4, as entered in the first column. The entries for the wedge density, G, corresponding to the first series of dial readings can then be entered at the top of the form as 0, 20.10, 60.20, 90.30, 120.40, and 150.50 (for convenience in calculations, the twolamp wedge density interval 0.3010 is multiplied by 100). The special calculations begin at the step R₁₃ to R₁₄, which is the central step between R₁₁ and R₂₁.

The step R₁₃ to R₁₄ gives us the first estimate for f₃:

f₃ = 30.1(R₁₄ - R₁₃)/(R₂₁ - R₁₁) = 30.1 x 5.9/29.3 = 6.06.

The first estimate for f₄ is

f₄ = 30.1(R₁₅ - R₁₄)/(R₂₂ - R₁₂) = 30.1 x 5.9/29.4 = 6.04.

One continues in this fashion down the remainder of the first column and down the next four main columns containing values of R. For instance, the first estimate of f₁ will be found to be

f₁ = 30.1(40.2 - 34.3)/(52.2 - 22.5) = 30.1 x 5.9/29.7 = 5.98.

The third estimate of f₃ will be found to be f₃ = 30.1(82.2 - 76.1)/(94.0 - 64.1) = 30.1 x 6.1/29.9 = 6.14.

The mean and adjusted values of f are given in the second last column and the accumulated values of f in the last column. From these by simple addition the provisional values of density are entered in the several rows for G immediately above the corresponding values for R. The full relationship of G to R can now be filled in to any required detail by a suitable standard method of interpolation.

Note: Since the first few steps from R₁₁ to R₁₃ are not central to any major interval, they cannot be used directly to estimate f₁ and f₂; the same is true for a few steps at the end. This does not prevent us from deducing values of density along the whole length of the wedge after all the steps f₁ to f₅ have been estimated.

A Wavelength Computation Form - Two Lamp Calibration
		DeltaR		DeltaR		DeltaR		DeltaR		DeltaR		Mean f Adj. f	Sum of f
G	0		30.10		60.20		90.30		120.40		150.50
R	5.0	29.3	34.3	29.8	64.1	29.9	94.0	29.8	123.8	29.7	153.5
deltaR			5.9		6.0		5.9		6.0
f1			5.98		6.02		5.98		6.08			6.02	6.02
G	6.02		36.12		66.22		96.32		126.42
R	10.8	29.4	40.2	29.9	70.1	29.8	99.9	29.9	129.8
deltaR			5.9		6.0		5.9		5.9
f2			5.98		6.02		5.98		5.98			5.99	12.01
G	12.01		42.11		72.21		102.51		132.41
R	16.6	29.5	46.1	30.0	76.1	29.7	105.8	29.9	135.7
deltaR	5.9		6.1		6.1		6.1		5.9
f3	6.06		6.16		6.14		6.16		5.98			6.30	18.11
G	18.11		48.21		78.31		108.41		130.51
R	22.5	29.7	52.2	30.0	82.2	29.7	111.9	29.7	141.6
deltaR	5.9		5.9		5.9		5.9		5.9
f4	6.04		5.94		5.96		5.94					5.97	24.08
G	24.08		54.18		84.28		114.38		144.48
R	28.4	29.7	58.1	30.0	88.1	29.7	117.8	29.7	147.5
deltaR	5.9		6.0		5.9		6.0		6.0
f5	6.02		6.02		5.98		6.04					6.02	30.10
												30.10
N.B. No adjustments to f values are necessary.

          The arbitrary constant is now fixed at a value to make (L₀ - L) or N equal to zero at that dial reading which one estimates would be obtained if the instrument could be taken outside the atmosphere for an observation of the sun on a S₂ / S₃ pair of wavelengths. The constant has to be determined for each wavelength pair and for each instrument separately, since it is dependent upon individual factors as well as the sun, e.g. slit widths and selectivity in scattering, reflection, and absorption at mirrors and at surfaces of prisms, lenses, photomultiplier, etc. As already mentioned, this constant is found generally by comparison with another previously calibrated instrument, although those stations which possess a long series of suitable observations can always check this constant by the method described in Appendix D. Appendix D also describes a method of transferring the calibration of a correctly calibrated spectrophotometer to the instrument with the newly calibrated optical wedge by means of standard lamps.

          When the provisional table for converting the dial readings to values of G (log I/I' + K) have been made, it is desirable to check their accuracy by converting some of the observations made during the two-lamp measurements back to values of G. For example, the values given previously can be converted as follows:

R2              40.2      55.1      80.5     109.5     130.6     156.6 
R1              10.8      25.4      50.5      79.8     100.7     126.9 
G2              36.2      51.13     76.61    106.00    127.22    153.60 
G1               6.02     21.04     46.51     75.91     97.14    123.50 
DeltaG          30.10     30.09     30.10     30.09     30.08     30.10

          DeltaG should equal 30.10 in all cases. The agreement is satisfactory.

3. Processing Optical Wedge Calibration Data by Computer

          Hand reduction of the two-lamp wedge calibration data described above involves considerable labor. A computer program, available from NOAA, Air Resources Laboratory, Boulder, Colorado, renders the task simple. For computer processing of the data, it is necessary first to plot the calibration data on a plot such as that shown in Figure 1, then to extract pertinent data from the graph for card punching on a coding form such as that shown in Figure 3. Final results are output in the form of wedge density tables, a sample of which is shown in Figure 4.

---

INST. NO. 83 APRIL 30, 1971
GA TABLE
R	0	1	2	3	4	5	6	7	8	9
0						0.0	1.1	2.1	3.2	4.3
10	5.3	6.4	7.5	8.5	9.6	10.7	11.7	12.8	13.8	14.9
20	16.0	17.0	18.1	19.1	20.2	21.2	22.2	23.3	24.3	25.3
30	26.4	27.4	28.4	29.5	30.5	31.5	32.5	33.5	34.5	35.5
40	36.6	37.5	38.5	39.5	40.5	41.5	42.5	43.4	44.4	45.3
50	46.3	47.3	48.2	49.2	50.1	51.1	52.0	52.9	53.9	54.8
60	55.8	56.7	57.6	58.6	59.5	60.4	61.4	62.3	63.2	64.2
70	65.1	66.0	67.0	67.9	68.8	69.7	70.7	71.6	72.5	73.5
80	74.4	75.3	76.2	77.2	78.1	79.0	80.0	80.9	81.9	82.8
90	83.7	84.7	85.6	86.6	87.5	88.5	89.4	90.3	91.3	92.2
100	93.2	94.1	95.1	96.0	97.0	97.9	98.9	99.8	100.8	101.7
110	102.6	103.6	104.5	105.5	100.4	107.4	108.3	109.2	110.2	111.1
120	112.1	113.0	114.0	114.9	115.9	116.8	117.8	118.7	119.7	120.6
130	121.6	122.5	123.5	124.4	125.4	126.3	127.3	128.3	129.2	130.2
140	131.1	132.1	133.1	134.0	135.0	136.0	136.9	137.9	138.9	139.9
150	140.8	141.8	142.8	143.8	144.7	145.7	146.7	147.7	148.6	149.6
160	150.6	151.6	152.6	153.5	154.5	155.5	156.5	157.5	158.4	159.4
170	160.4	161.4	162.4	163.4	164.4	165.4	160.4	167.3	168.3	169.3
180	170.3	171.3	172.3	173.3	174.3	175.2	176.2	177.2	178.2	179.2
190	180.2	181.1	182.1	183.1	184.1	185.1	186.0	187.0	188.0	189.0
200	190.0	191.0	192.0	192.9	193.9	194.9	195.9	196.9	197.9	198.9
210	199.9	200.9	201.9	202.9	203.9	204.9	205.9	206.9	207.9	208.9
220	209.9	210.9	211.9	212.9	213.9	215.0	216.0	217.0	218.0	219.0
230	220.0	221.0	222.1	223.1	224.1	225.1	226.1	227.2	228.2	229.2
240	230.2	231.3	232.3	233.3	234.3	235.4	236.4	237.4	238.5	239.5
250	240.5	241.5	242.5	243.6	244.6	245.6	246.6	247.6	248.7	249.7
260	250.7	251.7	252.7	253.8	254.8	255.8	256.8	257.8	258.9	259.9
270	260.9	261.9	262.9	263.9	264.9	266.0	267.0	261.9	269.0	270.0
280	271.1	272.1	273.1	274.1	275.2	276.2	277.2	278.3	279.3	280.3
290	281.4	282.4	283.4	284.5	285.5	286.6	287.6	288.7
INPUT DATA:
	28.47	28.63	28.87	29.24	29.74	30.26	30.78	31.26
	31.68	32.02	32.20	32.28	32.27	32.20	32.12	32.03
	31.95	31.89	31.85	31.03	31.82	31.17	31.67	31.54
	31.38	31.23	31.09	30.97	30.83	30.72	30.63	30.58
	30.55	30.54	30.56	30.55	30.52	30.46	30.35	30.22
	30.07	29.91	29.76	29.63	29.52	29.45	29.42	29.42
	29.45	29.51	29.51	29.54	29.48	29.37	29.22

Figure 4. Sample optical wedge density table for A wavelengths.

---

Return to Table of Contents

Forward to Appendix D. Calibrating a Spectrophotometer on an Absolute Scale